- - - APRENDIENDO MAS DE LA GEOMETRÍA Y LA MATEMÁTICA + + +
LAS REDES SOCIALES
ARQUIMEDES CIENTÍFICO
Arquímedes de Siracusa (en griego antiguo Siracusa (Sicilia), ca. 287 a. C. – ibídem, ca. 212 a. C.) fue un matemático griego, físico, ingeniero, inventor y astrónomo. Aunque se conocen pocos detalles de su vida, es
considerado uno de los científicos más importantes de la antigüedad clásica. Entre sus avances en física se encuentran sus fundamentos enhidrostática, estática y la explicación del principio de la palanca. Es reconocido por haber diseñado innovadoras
máquinas, incluyendo armas de asedio y el tornillo de Arquímedes, que lleva su nombre. Experimentos modernos han
probado las afirmaciones de que Arquímedes llegó a diseñar máquinas capaces de
sacar barcos enemigos del agua o prenderles fuego utilizando una serie de
espejos
ANGULO RECTO
EN ESTA PAGINA PODREMOS VER UNA CONSTRUCCIÓN EN GEOGEBRA
https://sites.google.com/site/lisethtrabajosdelcol/home/tareas-de-informatica
INVENTOS DE ARQUIMEDES
Inventos de Arquímedes
Sus Inventos y
descubrimientos
La corona dorada:
El rey había pedido como encargo una corona de oro y no
estaba muy seguro de que esta fuera exclusivamente de oro, así que pidió a
Arquímedes que lo averiguara.
Arquímedes tras muchas deliberaciones encontró la manera.
Sumergió un bloque de oro puro del mismo peso de la
corona y la misma corona en un tanque de agua si ambos objetos desalojaban el
mismo nivel de agua la corona estaría hecha de enteramente de oro. Finalmente
se descubrió que la corona no estaba hecha solo de oro y asesinaron al orfebre
por fraude.
El tornillo de Arquímedes
Se quería construir un barco de lujo, para cargas etc…
Pero el barco al ser de gran tamaño dejaría pasar grandes cantidades de agua.
Arquímedes inventó un tornillo con el cual pudiera
extraer grandes cantidades de agua de la sentina (que es la parte inferior de
los barcos) El tornillo se accionaba de forma manual.
La garra de Arquímedes
La garra de Arquímedes era un brazo similar a el de las
grúas que Arquímedes usó como arma de asedio contra los barcos romanos.
Los rayos de calor
Usando un sistema combinado con espejos y los rayos de
luz solar, con el que consiguió quemar las velas de los barcos romanos
La palanca
Arquímedes inventó la palanca, con la que podía mover
grandes objetos con poca fuerza. De ahí su frase célebre “dadme un punto de
apoyo y moveré el mundo”
http://www.youtube.com/watch?v=zCAzQmfd1Gc
BIOGRAFÍA DE ARQUIMEDES
Arquímedes, nace en Siracusa dos generaciones
después de Euclides (287–212 a.c.). Muchas de sus vivencias, han llegado hasta
nuestros días, al igual que muchos de sus trabajos matemáticos. Todas las
fuentes que le han descrito, coinciden en que era un genio excéntrico.
Hijo de astrónomo, desde joven se interesó por el estudio
de los cielos. Su impresionante talento matemático se incrementó por su
capacidad concentración. Llegaba a pasar largos periodos de tiempo trabajando.
Cuentan que se olvidaba de comer y descuidaba su persona hasta el punto de que
era obligado a bañarse a la fuerza.
SOBRE LA GEOMETRÍA
La geometría es una rama de las matemáticas que se ocupa
de las propiedades del espacio. En su forma más elemental, la geometría se
preocupa de problemas métricos como el cálculo del área y diámetro de figuras
planas y de la superficie y volumen de cuerpos sólidos.
Las matemáticas son el estudio de las relaciones entre
cantidades, magnitudes y propiedades, y de las operaciones lógicas utilizadas
para deducir cantidades, magnitudes y propiedades desconocidas.
Las matemáticas son tan antiguas como la propia
humanidad.
Las matemáticas avanzadas y organizadas fueron
desarrolladas en el tercer milenio a.C., en Babilonia y Egipto, las cuales
estaban dominadas por la aritmética, con cierto interés en medidas y cálculos
geométricos.
MATEMÁTICOS Y LA MÚSICA
Pitágoras y la música
La palabra matemáticas proviene del término griego Mathema,
que significa conocimiento.
Los pitagóricos dividieron esta ciencia en cuatro
secciones: aritmética, geometría, astronomía y música, que constituían la
esencia del conocimiento.
“Todas las cosas están también conformadas según los
números”
“Las propiedades y relaciones de la armonía musical están
determinadas por los números “
LA ESCALA
DIATÓNICA
Pitágoras estaba influenciado por sus conocimientos sobre
las medias (aritmética, geométrica y armónica) y el misticismo de los números
naturales, especialmente los cuatro primeros (tetrakis). Había experimentado
que cuerdas con longitudes de razones
1:2 (los extremos 1 y 2), 2:3 (media armónica de 1 y 2), y 3:4 (media
aritmética de 1 y 2) producían al hacerlas vibrar combinaciones de sonidos
agradables (armónicos) y construyó una escala a partir de estas proporciones:
3 : 4 es la media
aritmética de 1 y 1/2 :
2 : 3 es la media armónica de 1 y 1/2 :
Proporciones 1/1 1/2 2/3 3/4
Sonido Unísono Octava Quinta Cuarta
Hoy los llamamos octava,
quinta y cuarta porque corresponden a esas notas de la escala pitagórica
diatónica (do, re, mi, fa, sol, la, si, do).
MATEMÁTICAS Y SU APORTE A LA MÚSICA
Es común escuchar que “hay
Matemática en la Música porque cuando se abre una partitura ésta está llena de
numeritos”, es decir, de los números del compás y las digitaciones. Obviamente
esta observación es muy simple. Se dice que hay Matemática en la Música, que la
Música y la Matemática están muy relacionadas. Pero ¿hay Matemática en la
Música? ¿Están relacionadas? ¿Qué relación existe entre la Música y la
Matemática? (Pdf 2 Nb)Los sonidos musicales son producidos por algunos procesos
físicos que tienen un carácter periódico - una cuerda vibrando, el aire en el
interior de un instrumento de viento, etc. Aun siendo muy diferentes entre
ellos, estos procesos pueden ser descritos con un mismo modelo matemático. La
característica más fundamental de esos sonidos es su "altura" o
frecuencia. Documento elaborado por Andrés Volkov y Jorge Merino. (Doc 183 Kb)La
escala diatónica. Pitágoras estaba influenciado por sus conocimientos sobre las
medias (aritmética, geométrica y armónica) y el misticismo de los números
naturales, especialmente los cuatro primeros. Había experimentado que cuerdas
con longitudes de razones 1:2, 2:3 y 3:4
producían combinaciones de sonidos agradables y construyó una escala a partir
de estas proporciones. (Doc 97 Kb)
FUNCIÓN SENO
En trigonometría el seno de
un ángulo en un triángulo rectángulo se define como la razón entre el cateto
opuesto y la Hipotenusa
https://sites.google.com/site/lisethquinonesinformatiac/trigonometria
Origen Trigonometria
El origen de la palabra
trigonometría proviene del griego. Es la composición de las palabras griegas
trigonon: triángulo y metron: medida; trigonometría: medida de los triángulos.Se
considera a Hiparco (180-125 a.C.) como el padre de la trigonometría debido
principalmente por su hallazgo de algunas de las relaciones entre los lados y
los ángulos de un triángulo. También contribuyeron a la consolidación de la
trigonometría Claudio Ptolomeo y Aristarco de Samos quienes la aplicaron en sus
estudios astronómicos. En el año 1600, el profesor de matemáticas de Heidelberg
(la universidad más antigua de Alemania) Bartolomé Pitiscus (1561-1613),
publicó un texto con el título de Trigonometría, en el que desarrolla métodos
para la resolución de triángulos. El matemático francés François Viète
(1540-1603) hizo importantes aportes hallando fórmulas trigonométricas de
ángulos múltiples. Los cálculos trigonométricos recibieron un gran impulso gracias
al matemático escocés John Neper (1550-1617), quien inventó los logaritmos a
principios del siglo XVII. En el siglo XVIII, el matemático suizo Leonard Euler
(1707-1783) hizo de la trigonometría una ciencia aparte de la astronomía, para
convertirla en una nueva rama de las matemáticas.
HISTORIA DE LA TRIGONOMETRIA
La historia de la
trigonometría y de las funciones trigonométricas podría extenderse por más de
4000 años. Los babilonios determinaron aproximaciones de medidas de ángulos o
de longitudes de los lados de los triángulos rectángulos. Varias tablas
grabadas sobre arcilla seca lo testimonian. Así, por ejemplo, una tablilla
babilonia escrita en cuneiforme, denominada Plimpton 322 (en torno al 1900 a.
C.) muestra quince ternas pitagóricas y una columna de números que puede ser
interpretada como una tabla de funciones trigonométricas; 1 sin embargo,
existen varios debates sobre si, en realidad, se trata de una tabla
trigonométrica.
LA TAKETINA
Taketina es un proceso en
grupo, singular y musical. Activa el potencial musical y humano a través del
ritmo. La enseñanza de taketina abre a cada persona la puerta a su talento
rítmico. Transmite ritmo de una manera natural que cada cual aprende y comprende
en sí mismo. Es una forma de utilizar tu cuerpo y tu voz como en una
herramienta de música con el que puedes expresar desde tu cuerpo musica de
cualquier tipo.
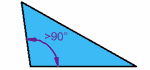
TRIÁNGULO ACUTÁNGULO
TRIÁNGULO ACUTÁNGULO:
Un triángulo que tiene todos sus ángulos menores a 90° (90° se llama ángulo recto)

TRIÁNGULO RECTÁNGULO
TRIÁNGULO RECTÁNGULO:
En geometría, se llama triángulo rectángulo a todo triángulo que posee un ángulo recto, es decir, un ángulo de 90-grados.1 Las relaciones entre los lados de un triángulo rectángulo es la base de la trigonometría. En particular, en un triángulo rectángulo se cumple el teorema de Pitágoras.

TRIÁNGULO ESCALENO
TRIÁNGULO ESCALENO:
Un triángulo con todos los lados de diferentes longitudes.
Ningún lado es igual a otro ni ningún ángulo es igual a otro.

TRIANGULO EQUILATERO
En geometría, un triángulo equilátero, es un triángulo con tres lados iguales. En la geometría euclídea tradicional, los triángulos equiláteros también son equiangulares, es decir, los tres ángulos internos también son congruentes entre sí, cada ángulo vale 60°. Un triángulo equilátero es un polígono regular; es un caso especial de triángulo isósceles.
DEFINICIÓN DE TRIANGULO
Un triángulo, en geometría, es un polígono determinado por tres rectas que se cortan dos a dos en tres puntos (que no se encuentran alineados). Los puntos de intersección de las rectas son los vértices y los segmentos de recta determinados son los lados del triángulo. Dos lados contiguos forman uno de los ángulos interiores del triángulo.
Por lo tanto, un triángulo tiene 3 ángulos interiores, 3 lados y 3 vértices.
DEFINICIÓN DE POLIGONOS
En geometría, un polígono es una figura plana que está limitada por una curva cerrada, compuesta por una secuencia finita de segmentos rectos. Estos segmentos son llamados lados, y los puntos en que se intersecan se llaman vértices. El interior del polígono es llamado a veces su cuerpo.
RECTA PARALELA Y RECTA PERPENDICULAR
RECTA PARALELA:
Dos rectas son paralelas si sus vectores directores son paralelos, es decir, si éstos son linealmente dependientes.
Dos rectas son perpendiculares cuando al cortarse forman cuatro ángulos iguales de 90º.
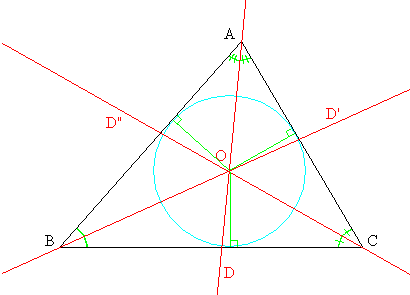
MEDIATRIZ Y BISECTRIZ
MEDIATRIZ:
La mediatriz de un segmento es la recta perpendicular a dicho segmento trazada por su punto medio. Equivalentemente se puede definir como la recta cuyos puntos son equidistantes a los extremos del segmento. También se la llama simetral. Lugar geometrico de los puntos que equidistan de los extremos de un segmento AB.
BISECTRIZ:
La bisectriz de un ángulo es la recta que lo divide en dos partes iguales. Es el lugar geométrico de los puntos del plano que equidistan (están a la misma distancia ) de las semirrectas de un ángulo.
ÁNGULOS Y CLASES DE ANGULOS
Un ángulo es la parte del plano comprendida entre dos semirrectas que tienen el mismo punto de origen o vértice.1 Suelen medirse en unidades tales como el radián, el grado sexagesimal o el grado centesimal.
Pueden estar definidos sobre superficies planas (trigonometría plana) o curvas (trigonometría esférica). Se denomina ángulo diedro al espacio comprendido entre dos semiplanos cuyo origen común es una recta. Un ángulo sólido es el que abarca un objeto visto desde un punto dado, midiendo su tamaño aparente.
CLASES DE ÁNGULOS:
Agudo < 90° Recto = 90° Obtuso>90°
Convexo < 180° Llano = 180° Cóncavo > 180°
Nulo = 0º Completo = 360°
Negativo < 0º Mayor de 360°
PUNTO,RECTA,SEMIRRECTA,SEGMENTO.
PUNTO:
En geometría, el punto es uno de los entes fundamentales, junto con la recta y el plano. Son considerados conceptos primarios, o sea, que sólo es posible describirlos en relación con otros elementos similares.
RECTA:
RECTA:
En geometría euclidiana, la recta o línea recta, se extiende en una misma dirección, existe en una sola dimensión y contiene infinitos puntos; está compuesta de infinitos segmentos (el fragmento de línea más corto que une dos puntos).
Una semirrecta es cada una de las partes en que queda dividida una recta por uno cualquiera de sus puntos.
Un segmento, en geometría, es un fragmento de recta que está comprendido entre dos puntos, llamados extremos.
HISTORIA DE LA TRIGONOMETRIA
la historia de la trigonometría y de las funciones trigonométricas podría extenderse por más de 4000 años. los babilonios determinaron aproximaciones de medidas de ángulos o de longitudes de los lados de los triángulos rectángulos. varias tablas grabadas sobre arcilla seca lo testimonian. así, por ejemplo, una tablilla babilonia escrita en cuneiforme, denominada plimpton 322 (en torno al 1900 a. c.) muestra quinceternas pitagóricas y una columna de números que puede ser interpretada como una tabla de funciones trigonométricas sin embargo, existen varios debates sobre si, en realidad, se trata de una tabla trigonométrica.
la historia de la trigonometría comienza con los babilonios y los egipcios. estos últimos establecieron la medida de los ángulos en grados, minutos y segundos. sin embargo, en los tiempos de la grecia clásica, en el siglo ii a.c. el astrónomo hiparco de nicea construyó una tabla de cuerdas para resolver triángulos. comenzó con un ángulo de 71° y yendo hasta 180° con incrementos de 71°, la tabla daba la longitud de la cuerda delimitada por los lados del ángulo central dado que corta a una circunferencia de radio r. no se sabe el valor quehiparco utilizó para r.
300 años después, el astrónomo tolomeo utilizó r = 60, pues los griegos adoptaron el sistema numérico (base 60) de los babilonios.
Suscribirse a:
Comentarios (Atom)