https://sites.google.com/site/lisethquinonesinformatiac/trigonometria
FUNCIÓN SENO
En trigonometría el seno de
un ángulo en un triángulo rectángulo se define como la razón entre el cateto
opuesto y la Hipotenusa
Origen Trigonometria
El origen de la palabra
trigonometría proviene del griego. Es la composición de las palabras griegas
trigonon: triángulo y metron: medida; trigonometría: medida de los triángulos.Se
considera a Hiparco (180-125 a.C.) como el padre de la trigonometría debido
principalmente por su hallazgo de algunas de las relaciones entre los lados y
los ángulos de un triángulo. También contribuyeron a la consolidación de la
trigonometría Claudio Ptolomeo y Aristarco de Samos quienes la aplicaron en sus
estudios astronómicos. En el año 1600, el profesor de matemáticas de Heidelberg
(la universidad más antigua de Alemania) Bartolomé Pitiscus (1561-1613),
publicó un texto con el título de Trigonometría, en el que desarrolla métodos
para la resolución de triángulos. El matemático francés François Viète
(1540-1603) hizo importantes aportes hallando fórmulas trigonométricas de
ángulos múltiples. Los cálculos trigonométricos recibieron un gran impulso gracias
al matemático escocés John Neper (1550-1617), quien inventó los logaritmos a
principios del siglo XVII. En el siglo XVIII, el matemático suizo Leonard Euler
(1707-1783) hizo de la trigonometría una ciencia aparte de la astronomía, para
convertirla en una nueva rama de las matemáticas.
HISTORIA DE LA TRIGONOMETRIA
La historia de la
trigonometría y de las funciones trigonométricas podría extenderse por más de
4000 años. Los babilonios determinaron aproximaciones de medidas de ángulos o
de longitudes de los lados de los triángulos rectángulos. Varias tablas
grabadas sobre arcilla seca lo testimonian. Así, por ejemplo, una tablilla
babilonia escrita en cuneiforme, denominada Plimpton 322 (en torno al 1900 a.
C.) muestra quince ternas pitagóricas y una columna de números que puede ser
interpretada como una tabla de funciones trigonométricas; 1 sin embargo,
existen varios debates sobre si, en realidad, se trata de una tabla
trigonométrica.
LA TAKETINA
Taketina es un proceso en
grupo, singular y musical. Activa el potencial musical y humano a través del
ritmo. La enseñanza de taketina abre a cada persona la puerta a su talento
rítmico. Transmite ritmo de una manera natural que cada cual aprende y comprende
en sí mismo. Es una forma de utilizar tu cuerpo y tu voz como en una
herramienta de música con el que puedes expresar desde tu cuerpo musica de
cualquier tipo.
TRIÁNGULO ACUTÁNGULO
TRIÁNGULO ACUTÁNGULO:
Un triángulo que tiene todos sus ángulos menores a 90° (90° se llama ángulo recto)
TRIÁNGULO RECTÁNGULO
TRIÁNGULO RECTÁNGULO:
En geometría, se llama triángulo rectángulo a todo triángulo que posee un ángulo recto, es decir, un ángulo de 90-grados.1 Las relaciones entre los lados de un triángulo rectángulo es la base de la trigonometría. En particular, en un triángulo rectángulo se cumple el teorema de Pitágoras.
TRIÁNGULO ESCALENO
TRIÁNGULO ESCALENO:
Un triángulo con todos los lados de diferentes longitudes.
Ningún lado es igual a otro ni ningún ángulo es igual a otro.
TRIÁNGULO ISÓSCELES
TRIÁNGULO ISÓSCELES:
Un triángulo con dos lados iguales.
Los ángulos opuestos a los lados iguales también son iguales.
TRIANGULO EQUILATERO
En geometría, un triángulo equilátero, es un triángulo con tres lados iguales. En la geometría euclídea tradicional, los triángulos equiláteros también son equiangulares, es decir, los tres ángulos internos también son congruentes entre sí, cada ángulo vale 60°. Un triángulo equilátero es un polígono regular; es un caso especial de triángulo isósceles.
DEFINICIÓN DE TRIANGULO
Un triángulo, en geometría, es un polígono determinado por tres rectas que se cortan dos a dos en tres puntos (que no se encuentran alineados). Los puntos de intersección de las rectas son los vértices y los segmentos de recta determinados son los lados del triángulo. Dos lados contiguos forman uno de los ángulos interiores del triángulo.
Por lo tanto, un triángulo tiene 3 ángulos interiores, 3 lados y 3 vértices.
DEFINICIÓN DE POLIGONOS
En geometría, un polígono es una figura plana que está limitada por una curva cerrada, compuesta por una secuencia finita de segmentos rectos. Estos segmentos son llamados lados, y los puntos en que se intersecan se llaman vértices. El interior del polígono es llamado a veces su cuerpo.
RECTA PARALELA Y RECTA PERPENDICULAR
RECTA PARALELA:
Dos rectas son paralelas si sus vectores directores son paralelos, es decir, si éstos son linealmente dependientes.
RECTA PERPENDICULAR:
Dos rectas son perpendiculares cuando al cortarse forman cuatro ángulos iguales de 90º.
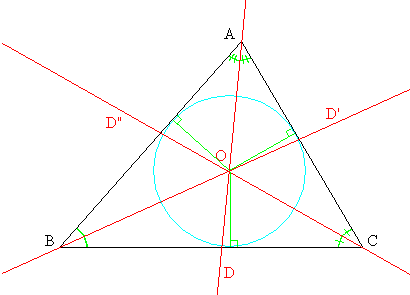
MEDIATRIZ Y BISECTRIZ
MEDIATRIZ:
La mediatriz de un segmento es la recta perpendicular a dicho segmento trazada por su punto medio. Equivalentemente se puede definir como la recta cuyos puntos son equidistantes a los extremos del segmento. También se la llama simetral. Lugar geometrico de los puntos que equidistan de los extremos de un segmento AB.
BISECTRIZ:
La bisectriz de un ángulo es la recta que lo divide en dos partes iguales. Es el lugar geométrico de los puntos del plano que equidistan (están a la misma distancia ) de las semirrectas de un ángulo.
ÁNGULOS Y CLASES DE ANGULOS
Un ángulo es la parte del plano comprendida entre dos semirrectas que tienen el mismo punto de origen o vértice.1 Suelen medirse en unidades tales como el radián, el grado sexagesimal o el grado centesimal.
Pueden estar definidos sobre superficies planas (trigonometría plana) o curvas (trigonometría esférica). Se denomina ángulo diedro al espacio comprendido entre dos semiplanos cuyo origen común es una recta. Un ángulo sólido es el que abarca un objeto visto desde un punto dado, midiendo su tamaño aparente.
CLASES DE ÁNGULOS:
Agudo < 90° Recto = 90° Obtuso>90°
Convexo < 180° Llano = 180° Cóncavo > 180°
Nulo = 0º Completo = 360°
Negativo < 0º Mayor de 360°
PUNTO,RECTA,SEMIRRECTA,SEGMENTO.
PUNTO:
En geometría, el punto es uno de los entes fundamentales, junto con la recta y el plano. Son considerados conceptos primarios, o sea, que sólo es posible describirlos en relación con otros elementos similares.
RECTA:
RECTA:
En geometría euclidiana, la recta o línea recta, se extiende en una misma dirección, existe en una sola dimensión y contiene infinitos puntos; está compuesta de infinitos segmentos (el fragmento de línea más corto que une dos puntos).
SEMIRRECTA:
Una semirrecta es cada una de las partes en que queda dividida una recta por uno cualquiera de sus puntos.
SEGMENTO:
Un segmento, en geometría, es un fragmento de recta que está comprendido entre dos puntos, llamados extremos.
HISTORIA DE LA TRIGONOMETRIA
la historia de la trigonometría y de las funciones trigonométricas podría extenderse por más de 4000 años. los babilonios determinaron aproximaciones de medidas de ángulos o de longitudes de los lados de los triángulos rectángulos. varias tablas grabadas sobre arcilla seca lo testimonian. así, por ejemplo, una tablilla babilonia escrita en cuneiforme, denominada plimpton 322 (en torno al 1900 a. c.) muestra quinceternas pitagóricas y una columna de números que puede ser interpretada como una tabla de funciones trigonométricas sin embargo, existen varios debates sobre si, en realidad, se trata de una tabla trigonométrica.
la historia de la trigonometría comienza con los babilonios y los egipcios. estos últimos establecieron la medida de los ángulos en grados, minutos y segundos. sin embargo, en los tiempos de la grecia clásica, en el siglo ii a.c. el astrónomo hiparco de nicea construyó una tabla de cuerdas para resolver triángulos. comenzó con un ángulo de 71° y yendo hasta 180° con incrementos de 71°, la tabla daba la longitud de la cuerda delimitada por los lados del ángulo central dado que corta a una circunferencia de radio r. no se sabe el valor quehiparco utilizó para r.
300 años después, el astrónomo tolomeo utilizó r = 60, pues los griegos adoptaron el sistema numérico (base 60) de los babilonios.
Suscribirse a:
Entradas (Atom)